كيفية حساب الانحراف المعياري
من المهم جدًا تعلم المهارات الرياضية واكتسابها وتوظيفها في حياتنا اليومية حيث أن العمليات الحسابية البسيطة تلزمنا كثيرًا وخصوصًا في عمليات البيع والشراء.
لا تقتصر أهمية دراسة الرياضيات على هذا الأمر بل تساعد التمارين الرياضية عمومًا على زيادة مستوى المهارات العقلية وتوظيف سرعة البديهة في حياتنا وترفع من ذكاء الأطفال.
كما تساعدنا على التفكير بمنطق وحكمة بشكل أكبر وحل أغلب المشكلات المعقدة التي قد تواجهنا.
تدخل الرياضيات في مهن كثيرة حيث أنه يمكن الاستفادة منها في تصميم الجرافيك من خلال معادلات الجبر الخطي، وأيضًا في الهندسة المعمارية حيث تعرفنا على مساحات التخطيط وغيرها من الأمور.
كما يمكن أن نقول أن علوم الحاسوب قائمة بأكملها على الرياضيات حيث يتم استخدام الخوارزميات وتطبيق العمليات الحسابية.
أي بالنهاية إن أي أمة تريد أن تتقدم وتزدهر يجب أن تهتم بمجال الرياضيات والعلوم لكي تحقق نتائج مهمة وتسير في درب الحضارة.
ومن أشهر المقولات التي تحدثت عن أهمية الرياضيات في الحياة:
يرتكز كل عالمنا على أسس رياضية: وهذه الأسس متشابكة على نحو غير ظاهر في ثقافتنا، بالمعنى العميق للكلمة.
ما هو الانحراف المعياري؟
إن الانحراف المعياري أو ما يعرف ب (Standard Deviation) هو مقدار يعبر عن انتشار البيانات وبعدها بالنسبة للوسط الحسابي الموجود.
يعبر عن الانحراف المعياري رمز هو (σ) ويتم حساب هذا المقدار عن طريق حساب الجذر التربيعي للتباين.
هناك فرق بين التباين والانحراف المعياري حيث أن الانحراف المعياري يقيس مقدار التشتت الموجود في البيانات ومدى اختلافها عن المتوسط الحسابي.
بالمقابل نجد أن التباين يقوم بوصف هذه الاختلافات كما أنه يحدد الانتشار الموجود في البيانات ومدى بعدها عن بعضها وعن المتوسط الحسابي للقيم.
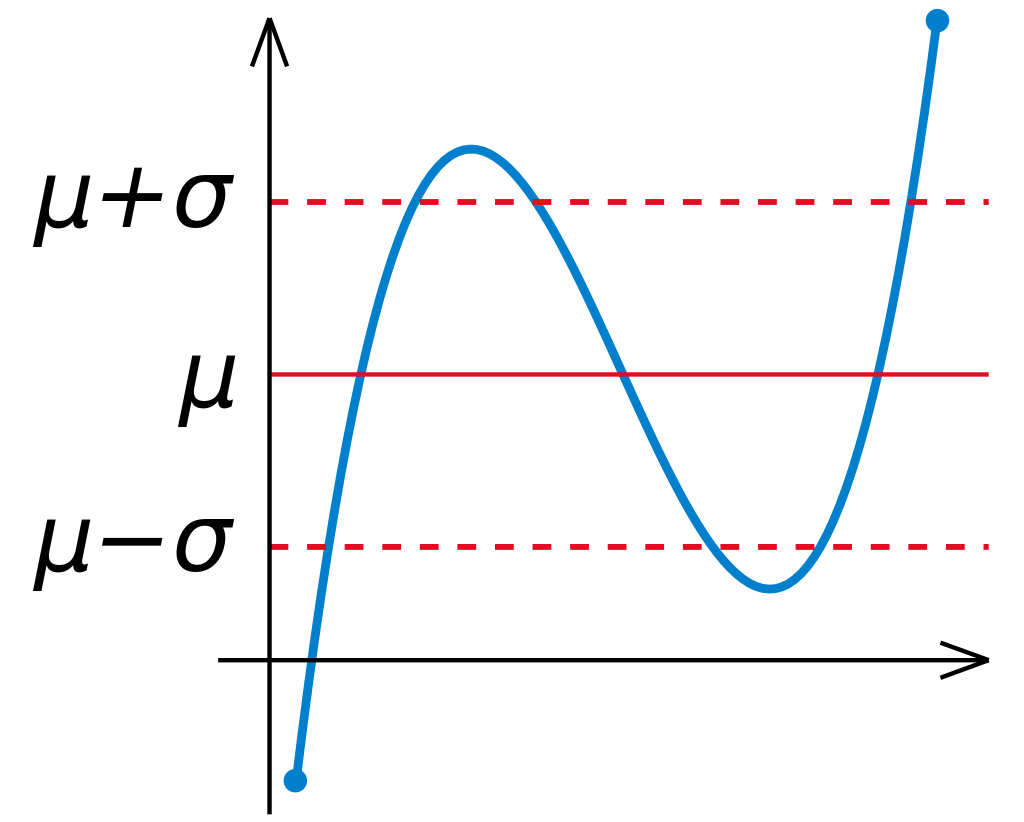
يشكل المتوسط الحسابي والانحراف المعياري سوية المخطط أو المنحنى الطبيعي لمجموعة القيم المدروسة ويكون المتوسط الحسابي محددًا المركز أو المنتصف أما الانحراف المعياري فيحدد عرض المنحنى الموجود.
ما هي أنواع الانحراف المعياري؟
هناك نوعين للانحراف المعياري هي كما يلي:
الانحراف المعياري لعينة ما من المجتمع:
يرمز لهذا النوع بالرمز ( S ) ونقوم باستخدامه عندما نرغب بدراسة الانحراف المعياري لمجموعة بيانات لا تمثل كامل البيانات الموجودة في المجتمع بسبب كثرة الأفراد.
نقوم بحساب هذا النوع وفق القانون التالي:
{مجموع ( س – الوسط الحسابي للعينة ) 2 / ( ن – 1 )} √
حيث أنّ:
ن : عدد القيم التي نقوم بدراستها.
س: هي القيم المشمولة في الدراسة التي نجريها.
الانحراف المعياري للمجتمع:
يمز لهذا النوع بالرمز (σ) وهو يستخدم عند دراسة بيانات مجتمع بأكمله ونستخدم ما يلي:
{مجموع ( س – μ )2 / ن} √
حيث أنّ:
ن : عدد القيم التي نقوم بدراستها.
س: كل القيم المشمولة في الدراسة التي نجريها.
μ: وهو المتوسط الحسابي للقيم الموجودة.
تمارين على الانحراف المعياري
المثال الأول:
لدينا مجموعة من الطلاب الذين تلقوا علاماتهم في مادة اللغة الإنكليزية وكانت العلامات كالتالي:
- عدد الطلاب الذين تتراوح علاماتهم بين 4 إلى 10 هو 3 طلاب.
- عدد الطلاب الذين تتراوح علاماتهم بين 10 و14 هو 6 طلاب.
- عدد الطلاب الذين تتراوح علاماتهم بين 14 و18 هو 4 طلاب.
- عدد الطلاب الذين تتراوح علاماتهم بين 18 و20 هو7 طلاب.
ما هو الانحراف المعياري لهذه القيم؟
حل التمرين:
| الفئة | مركز الفئة ( الحد الأعلى + الحد الأدنى ) ÷ 2 | التكرار الموجود |
| 8 – 4 | 6 | 3 |
| 12 – 8 | 10 | 6 |
| 16 – 12 | 14 | 4 |
| 20 – 16 | 18 | 7 |
الخطوة الأولى:
في البداية إذا أردنا حساب الانحراف المعياري يجب أن نحسب المتوسط الحسابي في البداية وهو كما يلي:
المتوسط الحسابي= (مركز الفئة × التكرار) / مجموع التكرارات
المتوسط الحسابي:
(3×6 + 6×10 + 4×14 + 7×18)/ 20 = 13
الخطوة الثانية:
نطبق قانون الانحراف المعياري وهو كما يلي:
الانحراف المعياري = [مجموع (التكرار×(مركز الفئة – المتوسط الحسابي)²)/مجموع التكرارات]√
[(3×(6-13)² + 6×(10-13)² + 4×(14-13)² + 7×(18-13)²)/20]√ = [(147+ 54 + 4 + 175)/20 ]√= 19√ =4.36
الجواب النهائي هو 4.36.
المثال الثاني:
احسب الانحراف المعياري للقيم التالية 1، 2 ، 3 ، 6 ؟
الحل:
الخطوة الأولى هي إيجاد المتوسط الحسابي.
المتوسط الحسابي= مجموع القيم / عددها = 3
الخطوة الثانية : نطبق قانون الانحراف المعياري وفق الجدول التالي
| القيمة | القيمة – المتوسط الحسابي | ( القيمة – المتوسط الحسابي)² |
| 6 | 3 | 9 |
| 3 | 0 | 0 |
| 2 | -1 | 1 |
| 1 | -2 | 4 |
| مجموع | 0 | 14 |
يكون الجواب النهائي هو:
(14/4 ) √ = 1.87
المثال الثالث:
احسب الانحراف المعياري للقيم التالية: 4 ، 9 ، 11 ، 12 ، 17 ، 5 ، 8 ، 12 ، 14 ؟
الخطوة الأولى ستكون حساب المتوسط الحسابي كما يلي:
( 4 + 9 + 11 + 12 + 17 + 5 + 8 + 12 + 14 ) / 9 = 10،222
الخطوة الثانية هي حساب الانحراف المعياري وفق القانون التالي:
{مجموع ( س – μ )2 / ن} √ وبتطبيق القانون:
الانحراف المعياري = 3.94
المثال الرابع:
احسب الانحراف المعياري للعينة التالية: 1، 2 ، 2 ، 6 ، 4 ؟
الخطوة الأولى هي إيجاد المتوسط الحسابي ونحسبه كما يلي:
6+4+2+2+1)/5 = 15/5 = 3
الخطوة الثانية هي حساب الانحراف المعياري عن طريق الجدول:
| القيم | القيمة – المتوسط الحسابي | ( القيمة – المتوسط الحسابي)² |
| 1 | 2 | 4 |
| 2 | -1 | 1 |
| 2 | -1 | 1 |
| 4 | -1 | 1 |
| 6 | 3 | 9 |
| المجموع | 0 | 16 |
بالتالي يكون الانحراف المعياري للقيم السابقة هو 2.
إن كل الأمثلة السابقة هي كلها تركز على أهمية الانحراف المعياري في الجوانب الحياتية والأنشطة العملية.
هكذا نكون قد وصلنا لنهاية مقالنا لليوم نرجو أن نكون قد وفقنا في تقديم معلومات مفيدة وقيمة للقارئ العزيز.