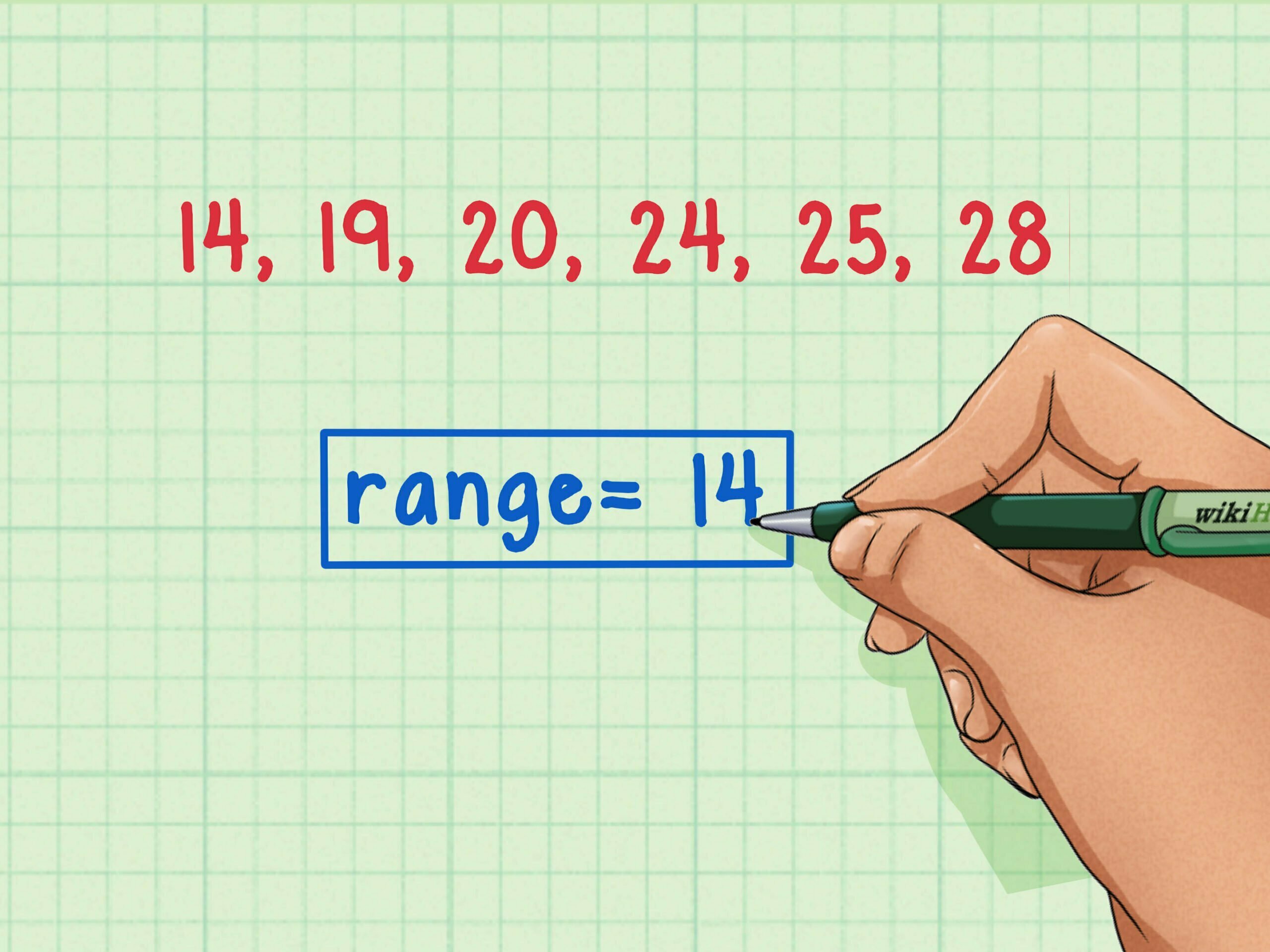كيفية حساب المدى والوسيط والمنوال

حساب المدى والوسيط والمنوال

إن مقياس النزعة المركزية يعتبر من أهم المفاهيم الإحصائية التي ظهرت في أواخر عشرينات القرن الماضي، وهو يتضمن مجموعة من القيم النموذجية والمركزية التي عن طريقها نقوم بتوزيع الاحتمالات، وفي بعض الأحيان تسمى بالمتوسطات أو مراكز التوزيع الإحصائية. هذه المقاييس تنقسم بصورة أساسية إلى المدى والمتوسط الحسابي والوسيط والمنوال.

إن أهم مقياس من المقاييس السابقة والأكثر استخدامًا نذكر مقياس المتوسط الحسابي الذي من خلاله يتم حساب مجموعة معينة من الأعداد النظرية. ويمكن القول أن مقاييس النزعة المركزية يتم استخدامها للدلالة على ميل الأعداد أو البيانات المدروسة لتتجمع حول قيم مركزية واحدة. من المهم أن نذكر أن كل مقاييس النزعة المركزية تختص بتلخيص العينات أو المجتمعات الإحصائية بقيم واحدة لتكون منتصف توزيع كل البيانات في الدراسة.

نستنتج مما سبق أن لهذه المقاييس أهمية كبيرة في مجالات متعددة مثل مجال العلوم المالية لكي يتم حساب قيمة دخل الفرد في مدينة واحدة. سنتعرف في هذا المقال على المتوسط الحسابي والوسيط والمنوال والمدى وسنتعرف على طرق حساب كل مقياس.

ما هو المتوسط الحسابي؟

هو المقياس الأهم من بين كل مقاييس النزعة المركزية ويتم استخدامه في كل عمليات الإحصاء وحساب النقطة التي تعتبر مكان تجمع ميل كل النقاط الأخرى.

إذا أردنا شرح مفهوم المتوسط بمعنى آخر فهو يعني المعدل مع تحديد مجموع الأعداد التي تعطى بنص المسألة ونقسم الناتج على عدد العناصر فنحصل على قيمة المتوسط الحسابي.

كمثال على المتوسط الحسابي لدينا المسألة التالية:

أوجد المتوسط الحسابي لمجموعة الأعداد الآتية (6، 2، 7، 2، 9)

الحل هو جمع القيم (9+2+2+7+6)=26 قسمة ناتج الجمع على عددها 26/5= 5. 2

كيفية حساب المدى والوسيط والنوال

نتحدث عن حساب المدى والوسيط والمنوال:

حساب الوسيط  Median

طريقة حساب الوسيط سهلة جدًا حيث يتم ترتيب القيم بشكل متصاعد أي من الأصغر وحتى الأكبر ومن ثم نوجد القيمة أو الرقم الذي يقع في المنتصف تمامًا.

إذا كان عدد العناصر التي نقوم بترتيبها زوجيًا فعندها يجب أن نأخذ القيمتين المتوسطتين ونجمعهما ثم نقسم على اثنين وهكذا نحصل على الوسيط لمجموعة العناصر أو البيانات المعطاة.

نأخذ مثال على عملية حساب الوسيط:

لدينا القيم المعطاة كالتالي: 8، 9، 15، 3، 12، 12 والمطلوب هو إيجاد الوسيط.

الحل: يمكن حل المسألة ب4 خطوات:

الخطوة الأولى: يجب عد القيم المعطاة، ومعرفة ما إذا كان عددها زوجي أو فردي، وفي المثال أعلاه لدينا عدد القيم رقم زوجي، لذلك من المتوقع إيجاد قيمتين في الوسط.

الخطوة الثانية: ترتيب القيم من الأصغر إلى الأكبر، كالتالي: 3، 8، 9، 12، 12، 15.

الخطوة الثالثة: علينا إيجاد القيمة المتوضعة في الوسط، وفي هذه الحالة يوجد رقمين وهما 9 و 12.

الخطوة الرابعة: إيجاد المتوسط الحسابي للقيم الواقعة في الوسط وذلك من خلال جمع القيمتين وتقسيمهما على 2:

9 + 12 = 21

21 ÷ 2 = 10.5

الوسيط = 10.5

اقرأ أيضًا: كيفية حساب الانحراف المعياري

حساب المنوال Mode

يعني مفهوم المنوال القيمة التي تتكرر في مجموعة الأعداد المتوفرة ضمن البيان الإحصائي، وقد يكون هناك عدة قيم متكررة بنفس العدد وفي هذه الحالة يكون لدينا أكثر من منوال في المسألة.

عندما يكون للبيانات الإحصائية منوالين نقول عنها ثنائية المنوال وإذا كان هناك أكثر من منوالين نسميها متعددة المنوال.

لاستخدام قيمة المنوال فائدة كبيرة جدًا حيث يمكن استخدامه عند فحص البيانات الفئوية مثل نكهات العلكة المصنعة أو نماذج السيارات، وقد يكون هناك بعض الحالات التي تكون فيها قيمة المنوال هي نفسها قيمة المتوسط الحسابي أو الوسيط.

هناك برنامج شهير يسمى إكسل قام بتطوير خاصية معينة لتحسب قيمة المنوال بطريقة بسيطة وتتسم بالسرعة.

سنذكر فيما يلي أمثلة على حساب قيمة المنوال:

المثال الأول:

لدينا القيم التالية المعطاة في نص المسألة وهي  7، 4، 5، 3، 9، 5، 2 والمطلوب هنا هو حساب قيمة المنوال:

نقوم بترتيب القيم من الأصغر وحتى الأكبر بهدف المساعدة على إيجاد قيمة المنوال بشكل بسيط وسريع وفي القيم السابقة المنوال هو رقم 5 لأنه تكرر مرتين بشكل واضح.

المثال الثاني:

لدينا القيم التالية المعطاة في نص المسألة  7، 4، 5، 3، 2، 5، 2 والمطلوب هنا أيضًا هو إيجاد قيمة للمنوال:

المنوال هنا هو ثنائي حيث لدينا الرقم 5 والرقم 2 قد تكرر كل منهما مرتين على عكس بقية القيم التي لم تكرر أبدًا.

اقرأ أيضًا: كل ما تحتاج لمعرفته عن نمط الوسيط INFP

حساب المدى Range

يمكن أن نعرف المدى على أنه الفرق بين القيمة الكبرى والقيمة الصغرى وهو يتأثر بشكل واضح بهاتين القيمتين ولكن لا يبدي أي علاقة بالقيم الأخرى الموجودة في نص المسألة.

إن المدى يعتبر أسهل مقياس من كل مقاييس النزعة المركزية حيث يحسب بسرعة وسهولة كبيرة ولا يهتم بالتوزيع التكراري على غرار بقية مقاييس النزعة المركزية.

لحساب المدى فوائد كبيرة حيث أنه يستخدم كثيرًا عند قياس فروقات درجات الحرارة بنفس المنطقة وأيضًا في استخراج معدلات نتائج الامتحانات.

عندما تكون قيمة المدى كبيرة جدًا فهذا يعني أن القيم المعطاة مشتتة ومتباعدة لدرجة كبيرة، وعلى العكس إذا ظهرت القيمة صغيرة فهذا يعني أن القيم متقاربة من بعضها البعض.

حساب قيمة المدى سهل جدًا وفي البداية يجب أن نرتب الأعداد المعطاة لنا بنص المسألة من الأصغر إلى الأكبر وبعدها نطرح القيمة الكبرى من القيمة الصغيرة وهكذا نحصل على القيمة المطلوبة.

مثال على ذلك لدينا المسألة التالية:

لدينا مجموعة الأرقام والبيانات التالية: 4، 6، 9، 3، 7 والمطلوب هنا هو إيجاد قيمة المدى:

بالبداية نقوم بترتيب البيانات الموجودة لدينا لسهولة الحساب ونحدد القيمة الكبيرة وهي 9 والقيمة الصغيرة وهي 3.

المدى = 9 – 3 = 6

مثال ثاني ببيانات وقيم جديدة هي (11، 16، 12، 13، 18، 16) والمطلوب هو إيجاد قيمة المدى الخاصة بما سبق.

نرتب القيم أولًا لسهولة الحساب ونحدد القيمة الكبيرة وهي 18 والقيمة الصغيرة وهي 11.

نطرح القيمة الكبيرة من القيمة الصغيرة ويكون الناتج لدينا هو 7.

هكذا نكون قد انتهينا من التعرف على مقاييس النزعة المركزية وطريقة حساب كل مقياس منهم نرجو أن نكون قد وفقنا في تقديم معلومات مفيدة وقيمة للقارئ العزيز.